NSK24034CE4C4S11轴承

图 6.1~6.5 所示的滚动轴承的外形尺寸定义了其几何结构。其中包括轴承公称内径 d、轴承外径D、宽度 B、轴承公称宽度（或装配高度）T、倒角尺寸 r 等。当将轴承安装在轴或轴承座上时，需知道所有这些尺寸。这些外形尺寸经过了国际标准化(ISO15)，并为 JIS B 1512（滚动轴承的外形尺寸）所采纳。向心轴承、圆锥滚子轴承及推力轴承的外形尺寸和尺寸系列，如表 6.1~6.3（A106~A115 页）。这些外形尺寸表格中列出了规定内径的各个内径代号，以及每个直径系列和尺寸系列的外形尺寸。我们可以提供大量的系列数量，但并不是所有都可以在市面上出售，因此，未来我们会添加更多的项目。每个轴承尺寸表（6.1~6.3）的顶部都是代表性的轴承类型和系列代号 （参考 A121页表 6.5 轴承系列代号）。图 6.6 和 6.7 所示分别为不同系列分类的向心轴承和推力轴承的截面尺寸（圆锥滚子轴承除外）。滚动轴承具有下列特点 ：(1) 启动摩擦小，且启动力矩与旋转力矩之差也较小。NSK24034CE4C4S11轴承

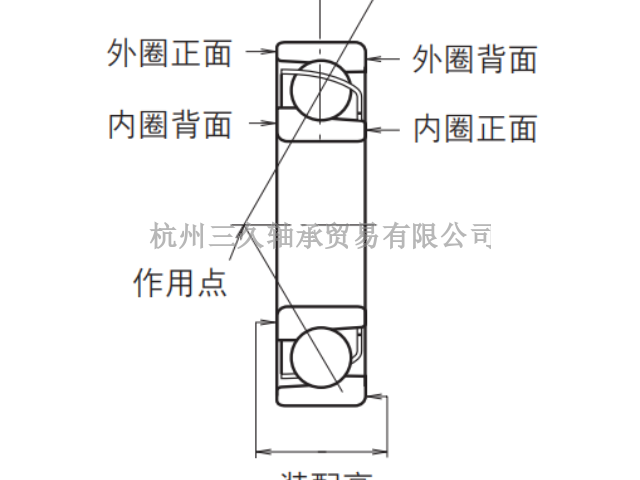
内部游隙与规格数值：运转过程中，滚动轴承内部游隙的大小对疲劳寿命、振动、噪声、发热等轴承性能影响很大。因此，在确定类型和尺寸后，选择轴承内部游隙便是轴承选择**重要的任务之一。轴承内部游隙是轴承内 / 外圈和滚动体之间的组合间隙量。所谓径向游隙和轴向游隙，即内圈或外圈一方固定，另一套圈相对其在径向和轴向上的移动量。为了获得精确的测量结果，通常会向轴承施加规定的测量载荷来测量游隙。因此，测出的游隙值（为了区别，有时也称为“测量 游隙 ”）总是比理论内部游隙（向心轴承也称“几何游隙”）大出测量载荷造成的弹性变形量。浙江NSK2909轴承重量通过调整内圈或外圈隔圈尺寸可获得合适的游隙。

当失效概率低于 10% 时（剩余概率≧ 90%），滚动疲劳寿命要长于韦布尔分布的理论曲线。这是基于对大量不同型号轴承进行寿命实验和数据分析得到的结论。由此考虑故障率≦ 10% 的轴承寿命时（例如，95% 寿命或 98% 寿命），则使用下表所示的可靠性系数 a1 确定寿命。假设额定疲劳寿命 L10 为10 000 小时的某一轴承，计算其可靠度为 98% 时的寿命 L2，可求得该寿命为 L2=0.33 x L10=3 300小时。通过此方法，可以将轴承寿命的可靠性与设备所要求的可靠性程度以及***检修和检查的难易程度相匹配。

当滚动轴承支撑的轴发生变形或轴肩精度不良时，轴承的内外圈之间便会出现倾斜，从而缩短疲劳寿命。疲劳寿命的缩短程度除了受轴承类型和内部设计的影响，还因使用时的径向内部游隙和载荷大小而异。采 用 标 准 设 计 的 圆 柱 滚 子 轴 承 NU215、NU315，其内、外圈倾斜与疲劳寿命之间的关系如图 4.35~4.38 所示。在这些图中，横轴表示为内 /外圈的倾斜 (rad)，纵轴表示疲劳寿命比 Lq /Lq=0。无倾斜的疲劳寿命为 Lq=0，有倾斜的疲劳寿命为 Lq。为在恒定载荷（轴承基本额定载荷的 10%）作用下，内部游隙分别为标准游隙、C3 游隙、C4游隙时的情况。图 4.37和图 4.38则是在恒定游隙（标准游隙）时，载荷分别为 5%Cr、10% Cr、20% Cr 时的情况。单列深沟球轴承，是滚动轴承中典型的一种结构形式，用途广。

市场对各种使用滚动轴承的机械设备、仪器等的性能要求日趋严格，对轴承要求的条件、性能也日趋多样化。为了能从众多的结构、尺寸中选择**适合的轴承，需要从各种角度研究。在轴承选型时，通常，考虑作为轴系内的轴承配制、安装、拆卸的难易度、轴承占用的空间、轴承尺寸及轴承的市场性等，大致决定轴承结构。其次，通过比较研究各种使用轴承的机械的设计寿命和各种轴承的不同耐久程度，从而决定轴承尺寸。在轴承选型时，往往只考虑轴承的疲劳寿命，但由润滑脂老化而引起的润滑脂寿命、磨损、噪声等也需要充分考虑。此外，还要根据不同用途对精度、游隙、保持架结构、润滑脂等提出特殊的设计要求。主要用于小型发电机、陀螺仪、计量仪器等。NSK24040CE4C3S11轴承卖价

单列深沟球轴承摩擦力矩小，适于高转速、低噪音、低振动的场合。NSK24034CE4C4S11轴承

因此，NSK 新寿命计算公式考虑到了清洁环境和低载荷区域中寿命测试结果的趋势。根据该等结果可得出新寿命公式的函数为 (P-Pu)/C，其受润滑参数确定的具体润滑条件影响。此外，据推测，不同类型和形状异物颗粒的作用受既存轴承载荷和润滑条件的影响很大，该关系可以表示为载荷参数的函数。新寿命计算公式的关系由 (P-Pu)/C·1/ac 定义。根据以上这一概念，可得出表面起点型剥落的计算公式，具体如下：ln 1S ∝ NeV(τ−τu)cZoh dV × { 1f(ac,aL) –1} ....(4.11)NSK24034CE4C4S11轴承